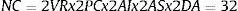Both clinical trials and clinical observational studies are designed to answer one or more research questions. Inherent to the research question is the study of one or more exposures (treatment, health habit) and one or more health effects, which are formulated as a research hypothesis. To test this hypothesis, a study is designed and performed to generate data. In the analysis phase, these data are compared with the initially proposed hypothesis, and the appropriate statistical tests are applied according to the nature of the independent and dependent variables.
If differences in the response variable (depending on the level of exposure, e.g. treatments) are observed in the statistical analysis, these may be due to: 1) the real effect of the treatment; 2) a bias; and/or 3) random error (chance).1 Statistics help us quantify the probability that differences between exposures are due to a random error in the process of selecting the study sample. We must remember that the subjects included in a study are actually a sample of the study population, and that from this population, infinite samples can be drawn, all of which will be different from each other, and potentially different from the overall population. Therefore, the study sample may differ randomly from the population.
Statistics use hypothesis testing to calculate the probability that, if such differences between treatments did not exist in the population, we would have found them in our data by chance. If this probability is less than the probability established a priori (alpha risk = 0.05), we can conclude with a 95% certainty that this difference also exists in the population. But this also means that we have a 1 in 20 chance of concluding wrongly that there are differences in the population, when in reality there are none (false positive).
The problemThe problem arises when we make multiple unplanned comparisons. The more comparisons we make, the greater the likelihood that one of them will be a false positive.2 If (NC) is the number of comparisons, the probability of finding at least one statistically significant association by chance is: 1-(0.95)NC. Thus, if 25 comparisons are made, the probability of finding a false positive rises from 5% to 72%. And this can be especially problematic when statistically significant results are selectively published,3 as the probability that they are due to chance is close to one.
Main methods of making multiple comparisons in clinical trialsInclude new response variablesThe research question of a trial usually involves a single primary response variable, although researchers often analyze others that were not originally planned, especially when the outcomes of the initial response variable are not as expected when the hypothesis was proposed. Other variables are sought or newly constructed from existing variables to “see if something statistically significant emerges”. This increases the risk of finding false positives.
To prevent this, authors should avoid including unplanned outcome variables and, if they do, make it clear that the analysis is post-hoc. Moreover, they must show all comparisons made,2 to avoid the selective publication of statistically significant results. To avoid biased interpretation due to selective publication, readers, reviewers and editors must check that the outcome variables were stated a priori in the trial methodology and registration. Multiple trial registries have been set up,4–6 but sometimes (depending on the country and year of completion) details on the construction of the outcome variables may be insufficient.
The categorization of response variables is also prone to post-hoc opportunistic selection based on the most striking results. Therefore, it would be interesting to establish cut-off points in the protocol or to use internationally accepted standards.7
Subgroup analysisUnlike group analysis (defined a priori by the research question), in subgroup analysis, subgroups are usually defined afterwards (after data collection is complete). The subgroup analysis evaluates the effects of treatment on subpopulations of patients according to baseline clinical (e.g. diabetes, severity) or personal (sex, age, genetics) characteristics. The aim is to assess whether the treatment effect varies depending on certain patient characteristics.
Controversy exists over whether these evaluations should be performed8: not performing them may deprive us of new scientific knowledge, while performing them increases the possibility of obtaining false positives by the use of multiple comparisons.
Recommendations for considering subgroup analyses are9:
- (1)
If the subgroup analysis is included in the protocol, and the numbers undergoing this analysis are reduced.
- (2)
Use interaction calculations to assess heterogeneity between groups. The level of statistical significance of interactions can be used to assess whether chance can explain differences between subgroups.
- (3)
The results are consistent with other studies and are biologically plausible.
These are data analyses performed before the end of the study in order to generate preliminary results for deciding whether or not to discontinue the study. The main reasons for stopping a study are9: 1) a drug is determined to be harmful or 2) highly beneficial, or 3) the probability of demonstrating efficacy is negligible. This decision should be made by an independent data monitoring committee and not by the investigators themselves. In any case, it should be emphasized that even in this case, and despite the correction of the level of significance by statistical techniques such as O’Brien-Fleming, Peto or Pocock,9 estimates of the treatment effect will always be biased.
Other methodological aspects that can increase the type I error of a trial are the approach to missing data (different statistical methods can be used) and losses to follow-up (intent-to-treat or per-protocol).
ConclusionThere are many ways to make unplanned comparisons, using different response variables, different ways of grouping or categorizing the population, intermediate analyses, and subgroup analyses, or different ways of handling missing data or losses to follow-up.
None of these approaches needs to be used in isolation, and combinations can be made, multiplying the possibilities of unplanned comparisons. Thus, in the conservative case of testing just 2 response variables (VR) and 2 cut-off points (PC), with an intermediate and final analysis (AI), and 2 subgroup analyses (AS), testing 2 ways of processing the missing data (DA), the final number of combinations is:
In this way, the probability of coming up with a false positive rises from 5% to 81% (1 – 0.95NC = 0.81). And, if the author only shows “statistically significant” results in the article, the chance that this finding is a false positive is very high. This can be especially serious for public and clinical health if decisions are based on these false positives.
It is therefore particularly important that all statistical analyses are planned a priori, and that all analyses to be carried out are detailed in the trial registries. Editors, reviewers, and readers can then compare what is published with what was planned and assess the extent to which the outcome may be due to a false positive.
Please cite this article as: Piñeiro-Lamas M, Taracido M, Figueiras A. La ruleta rusa de los análisis estadísticos de estudios clínicos. Una reflexión para lectores y autores. Arch Bronconeumol. 2020;56:547–548.