Proper reference values for lung function testing are essential for achieving adequate interpretations. The LMS procedure (lambda, mu, sigma) permits continuous analyses of entire populations avoiding gaps in the transition between childhood and adulthood. It also allows more precise calculations of average values, dispersion, and 5th percentiles, which are usually considered the lower limit of normality. The objective of this study was to compare our results fitted with the LMS method with standard multiple linear regression, and with those from international Global Lung Function Initiative (GLI) equations.
MethodsData from 9835 healthy residents of the metropolitan area of Mexico City aged 8–80 years were compiled from several studies: EMPECE, PLATINO, adult Mexican workers and two unpublished studies. The LMS procedure and multiple linear regression models were fit to obtain reference equations using R software.
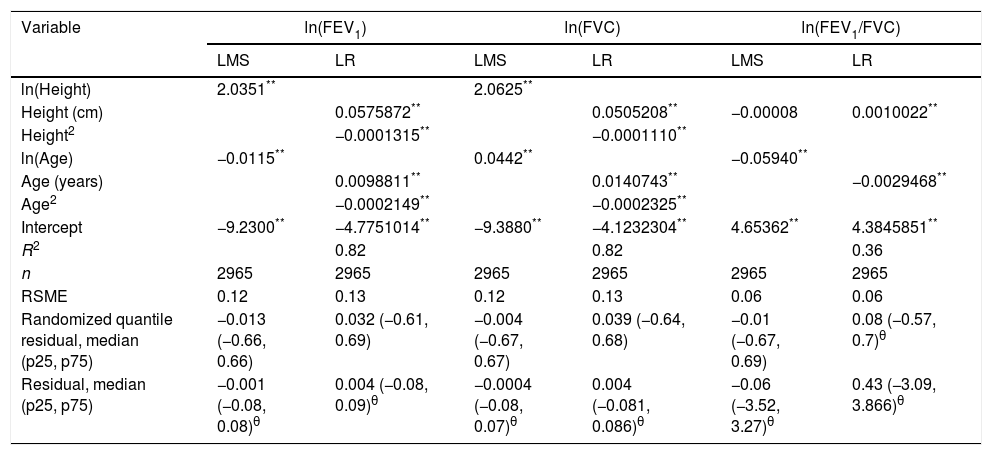
ResultsResiduals from the LMS models had a median closer to zero, and smaller dispersion than those from the linear model, but differences although statistically significant were very small and of questionable practical relevance. For example, for females and ln(FEV1), median residual was −0.001 with p25 of −0.08 and p75 of 0.08 for LMS, compared with 0.004 (−0.08, 0.09) [p<0.05] for the linear model. Average spirometric values for a given height for our population, were higher than those predicted by the GLI study.
ConclusionContinuous reference equations for the Mexican population calculated using the LMS technique showed slightly better fit than linear regression models.
Unos valores de referencia apropiados para las pruebas de la función pulmonar son esenciales para realizar unas interpretaciones adecuadas. El método LMS (lambda, mu, sigma) permite realizar análisis continuos de poblaciones enteras evitando brechas en la transición entre la infancia y la edad adulta. También permite cálculos más precisos de valores medios, dispersiones y percentiles 5, que generalmente se consideran el límite inferior de la normalidad. El objetivo de este estudio fue comparar nuestros resultados ajustados con el método LMS con la regresión lineal múltiple estándar y con los de las ecuaciones internacionales de la Iniciativa Global de Función Pulmonar (GLI).
MétodosSe recopilaron datos de 9.835 residentes sanos del área metropolitana de la Ciudad de México con edades comprendidas entre 8 y 80 años a partir de varios estudios: EMPECE, PLATINO, trabajadores adultos mexicanos y 2 estudios no publicados. El método LMS y los modelos de regresión lineal múltiple se ajustaron para obtener ecuaciones de referencia utilizando el software R.
ResultadosLos residuos de los modelos LMS tuvieron una mediana más cercana a cero y una dispersión menor que las del modelo lineal, pero las diferencias, aunque estadísticamente significativas, fueron muy pequeñas y de una relevancia práctica cuestionable. Por ejemplo, para las mujeres y el ln(FEV1), la mediana residual fue de −0,001 con p25 de −0,08 y p75 de 0,08 para LMS, en comparación con 0,004 (−0,08, 0,09) (p<0,05) para el modelo lineal. Los valores espirométricos medios para una altura dada para nuestra población fueron más altos que los pronosticados por el estudio GLI.
ConclusiónLas ecuaciones de referencia continua para la población mexicana calculadas usando la técnica LMS mostraron un ajuste ligeramente mejor que los modelos de regresión lineal.
Respiratory function tests are a very important component of patient assessment, but to achieve correct interpretations it is essential to compare the values found with a standard or reference.1 Reference values are useful and reliable to the extent that the process through which they are generated follows an accepted methodology regarding the equipment used, testing methods, selection of subjects and interpretation, as publications on the standardization of spirometry have described.2 Numerous reference values have been published, but their study populations have been selected in different ways and they may have utilized inadequate equipment and heterogeneous procedures, so the result is that their respective predicted values differ and produce differences in interpretation. In addition, reference values for children and adults are separated abruptly, perhaps because these two population sectors are cared for by different medical specialists, but it is also common to find that the levels determined for subjects aged just before, or just after, the cut-off point – usually between 18 and 20 years – do not fit well with the values predicted by the separate equations applied to children and adults.3
In addition to age, gender, body size, height, weight and ethnic factors may also contribute to the variability in test results. For this reason, specific values have also been generated for different ethnic groups. In one of the most successful efforts to organize this field, Haankinson and collaborators3 generated a population sample from childhood to old age that was divided into well-defined ethnic groups, as follows: Caucasians, Mexican-Americans and African-Americans, all residing in the United States. The group of African-Americans systematically had lower spirometric values for the same age and height as the other two groups; however, the reference values for children and adults were separated at 18 years of age. More recently, the Global Lung Function Initiative (GLI) project described spirometric reference equations that are continuous from childhood to old age and adjusted for various ethnic groups. In the event that significant variation arises, the GLI guidelines describe adjustments for the equation that produce greater order and can simplify the use of the reference values,4–6 but the Mexican population was left out of the GLI project because it was found to have significant differences from all other populations analyzed.4 The reasons for this are not yet clear, but the results were replicated in a longitudinal study of children.7 Therefore, the objectives of this study were to analyze spirometry from childhood to old age in a Mexican population using the GLI project methodology and linear regression models, and then compare results to those obtained by similar methods but based on diverse international populations.
MethodsMost of the data used in the present work were published previously, so they include diverse populations. The study incorporated data on adults aged 40+ from a population sample of the PLATINO project,8,9 children and adolescents aged 8–20 from the EMPECE study of school-children taken from a random sample of schools in the metropolitan area of Mexico City,10 adult workers aged 20–75,11 evaluated at the pulmonary function laboratory at the National Institute of Respiratory Diseases, and healthy participants in the 4–15 and 20–35 age group were recruited to complete the group of participants from two unpublished studies approved by the ethics committee of the institute, with numbers C26-17 and C28-13, respectively.
The PLATINO study, and the unpublished 4–15 years of age population, we utilized an ultrasonic spirometer (EasyOne on-PC, NDD, Zurich, Switzerland), while the EMPECE and adult workers’ studies occupied a dry-seal volume spirometer (model 922, SensorMedics, Yorba Linda, CA). The unpublished, 20–35 years of age participants, were tested with a pneumotachograph-based equipment (Ergospirometry 5.22.1.149, CareFusion, San Diego, California). All spirometers were tested daily for calibration with a 3l syringe, for volume, and the linearity of their sensors was verified once a week. All spirometers utilized meet current international standards and are very precise.
The procedures followed were quite similar and included up to 8 forced expiratory maneuvers to obtain 3 acceptable, and reproducible. All the personnel who performed testing had spirometry training course certified by the National Institute for Occupational Safety and Health (NIOSH) and followed international criteria current at the moment of the testing: for the EMPECE and workers’ studies the ATS 2003 quality criteria,12 and for the PLATINO study and remaining tests the 2005 ATS/ERS quality criteria.2
All recruited individuals were healthy from the respiratory point of view: never smokers (<100 cigarettes in lifetime), lacked respiratory symptoms (cough, phlegm, wheezing or dyspnea from a questionnaire), lacked previous physician diagnosis of asthma, COPD, chronic bronchitis, emphysema, tuberculosis, lung cancer or thoracic surgery, and were non-obese: in childrenkg/m2. Ethnic origin is usually not included in surveys applied in Mexico City, and all participants were considered to be Mexican mestizos.
The participants from EMPECE study and the PLATINO study, were representative samples of the school children and adult populations respectively, from metropolitan Mexico City. Recently studied healthy children aged 4–15 years from Metropolitan Mexico City were recruited from schools during 2014–2015, and the participants for 20–35 age group were volunteers, employees of our institution, their relatives, and students of medicine, respiratory care, and nursing from this institute.
Statistical analysisPrediction models were fitted for the best forced expiratory volume in 1s (FEV1), forced vital capacity (FVC), and their quotient (FEV1/FVC) to generate the lambda, mu, sigma (LMS),5,13,14 which calculate, separately, the average value (mu), the deviation around the central value (sigma), and the bias (lambda), depending on the age, sex and height of subjects, using a routine in the R language described by T.J. Cole and available on the GLI website.5,13,14 This technique avoids in principle problems associated with the linear regression technique, usually used to construct reference values: assumes homoscedasticity and a constant deviation around the average value, and in addition predicting equations have been published separately for children the period of growth in lung function with ascending values, and for adults with descending values. The LMS technique has also been used to generate growth curves in children (for height, weight and the body mass index).15 The routine described was modified minimally and only to make it compatible with the most up-to-date version of R.
We fitted the LMS and linear regression models using untransformed and log-transformed dependent and independent variables for each spirometric variable stratifying by gender. The best linear regression model was selected based on the coefficient of determination (r2) and lack of homoscedasticity. The LMS models were fitted using the Box-Cox-Cole-Green (BCCG) distribution and the lowest Bayesian information criterion (BIC) was considered to choose the best model. Conventional and randomized quantile residuals were used to compare LMS and linear models.
Subsequently, the values obtained from the sample were compared to both those reported in the GLI study and previously-reported reference values for Mexican populations.4,10,11
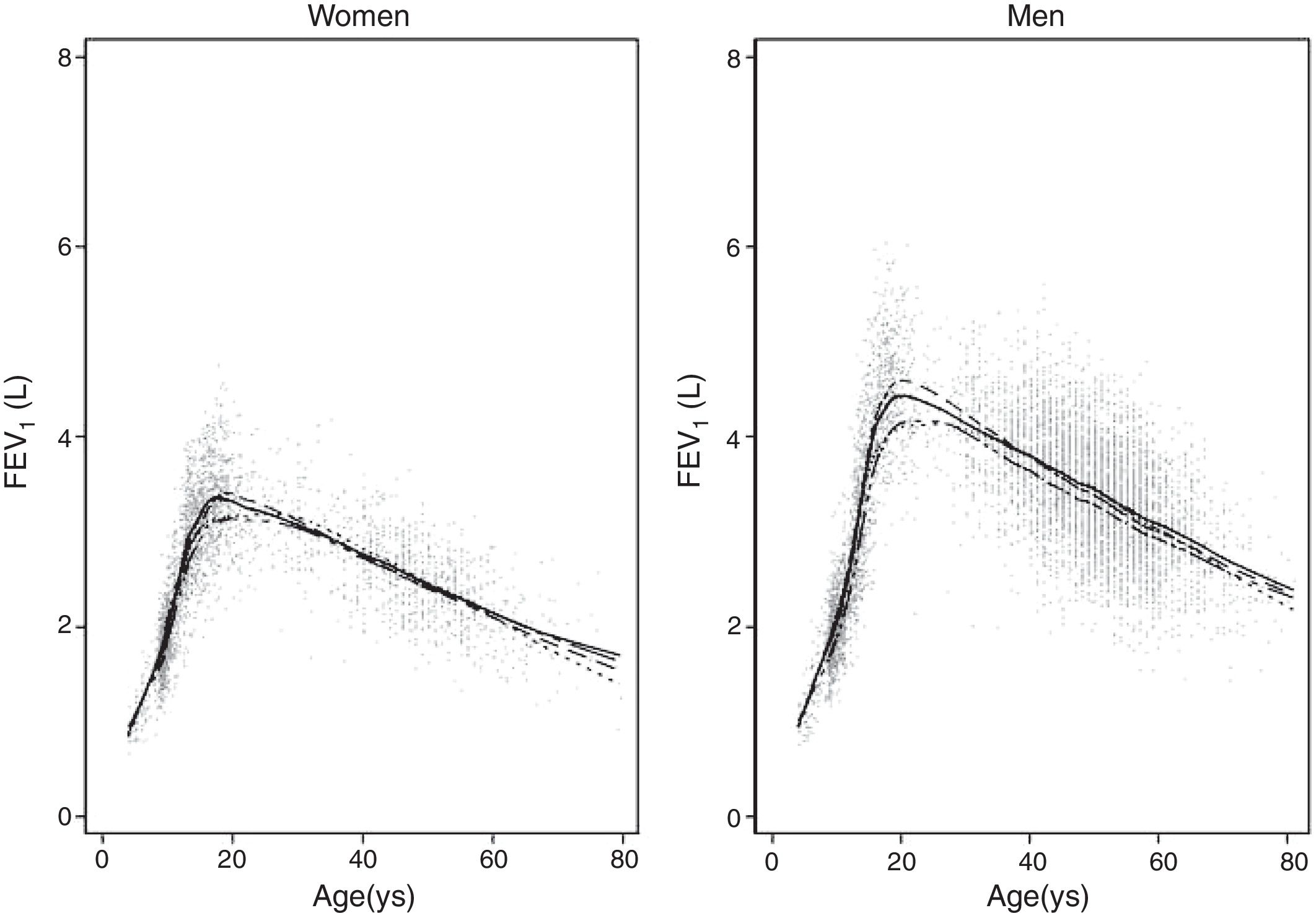
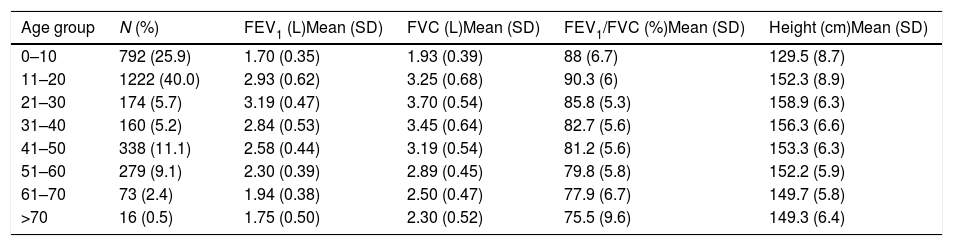
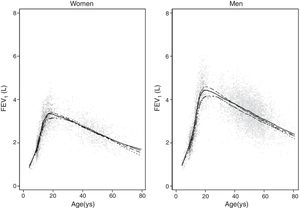
ResultsA total of 9835 subjects were included in the present study: 223 from the PLATINO project, 3995 from the EMPECE study, 4710 from the study of Mexican workers, and 907 obtained ex-professo for this analysis. Tables 1 and 2 present the spirometric variables and height by gender and age group. A sizable sample was obtained for each decade of age, and the growth and decline of lung function are clearly visible for both genders. Fig. 1 shows the FEV1 for the entire sample, where the various spirometric test results obtained from the different groups clearly seem to match well and connect correctly.
Descriptive statistics of the female subjects (N=3054).
| Age group | N (%) | FEV1 (L)Mean (SD) | FVC (L)Mean (SD) | FEV1/FVC (%)Mean (SD) | Height (cm)Mean (SD) |
|---|---|---|---|---|---|
| 0–10 | 792 (25.9) | 1.70 (0.35) | 1.93 (0.39) | 88 (6.7) | 129.5 (8.7) |
| 11–20 | 1222 (40.0) | 2.93 (0.62) | 3.25 (0.68) | 90.3 (6) | 152.3 (8.9) |
| 21–30 | 174 (5.7) | 3.19 (0.47) | 3.70 (0.54) | 85.8 (5.3) | 158.9 (6.3) |
| 31–40 | 160 (5.2) | 2.84 (0.53) | 3.45 (0.64) | 82.7 (5.6) | 156.3 (6.6) |
| 41–50 | 338 (11.1) | 2.58 (0.44) | 3.19 (0.54) | 81.2 (5.6) | 153.3 (6.3) |
| 51–60 | 279 (9.1) | 2.30 (0.39) | 2.89 (0.45) | 79.8 (5.8) | 152.2 (5.9) |
| 61–70 | 73 (2.4) | 1.94 (0.38) | 2.50 (0.47) | 77.9 (6.7) | 149.7 (5.8) |
| >70 | 16 (0.5) | 1.75 (0.50) | 2.30 (0.52) | 75.5 (9.6) | 149.3 (6.4) |
SD: standard deviation; FEV1: forced expiratory volume in 1s; FVC: forced vital capacity; FEV1/FVC: ratio of FEV1 to FVC.
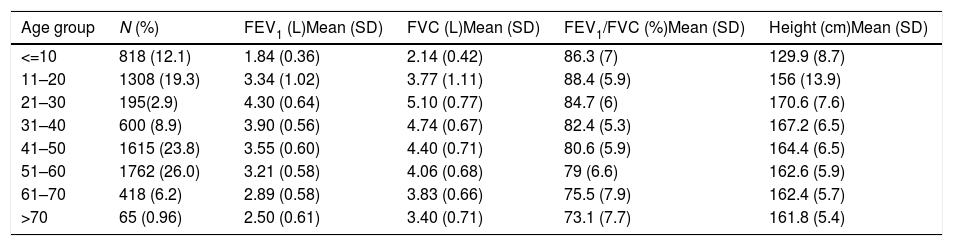
Descriptive statistics of the male subjects (N=6781).
| Age group | N (%) | FEV1 (L)Mean (SD) | FVC (L)Mean (SD) | FEV1/FVC (%)Mean (SD) | Height (cm)Mean (SD) |
|---|---|---|---|---|---|
| <=10 | 818 (12.1) | 1.84 (0.36) | 2.14 (0.42) | 86.3 (7) | 129.9 (8.7) |
| 11–20 | 1308 (19.3) | 3.34 (1.02) | 3.77 (1.11) | 88.4 (5.9) | 156 (13.9) |
| 21–30 | 195(2.9) | 4.30 (0.64) | 5.10 (0.77) | 84.7 (6) | 170.6 (7.6) |
| 31–40 | 600 (8.9) | 3.90 (0.56) | 4.74 (0.67) | 82.4 (5.3) | 167.2 (6.5) |
| 41–50 | 1615 (23.8) | 3.55 (0.60) | 4.40 (0.71) | 80.6 (5.9) | 164.4 (6.5) |
| 51–60 | 1762 (26.0) | 3.21 (0.58) | 4.06 (0.68) | 79 (6.6) | 162.6 (5.9) |
| 61–70 | 418 (6.2) | 2.89 (0.58) | 3.83 (0.66) | 75.5 (7.9) | 162.4 (5.7) |
| >70 | 65 (0.96) | 2.50 (0.61) | 3.40 (0.71) | 73.1 (7.7) | 161.8 (5.4) |
SD: standard deviation; FEV1: forced expiratory volume in 1s; FVC: forced vital capacity; FEV1/FVC: ratio of FEV1 to FVC.
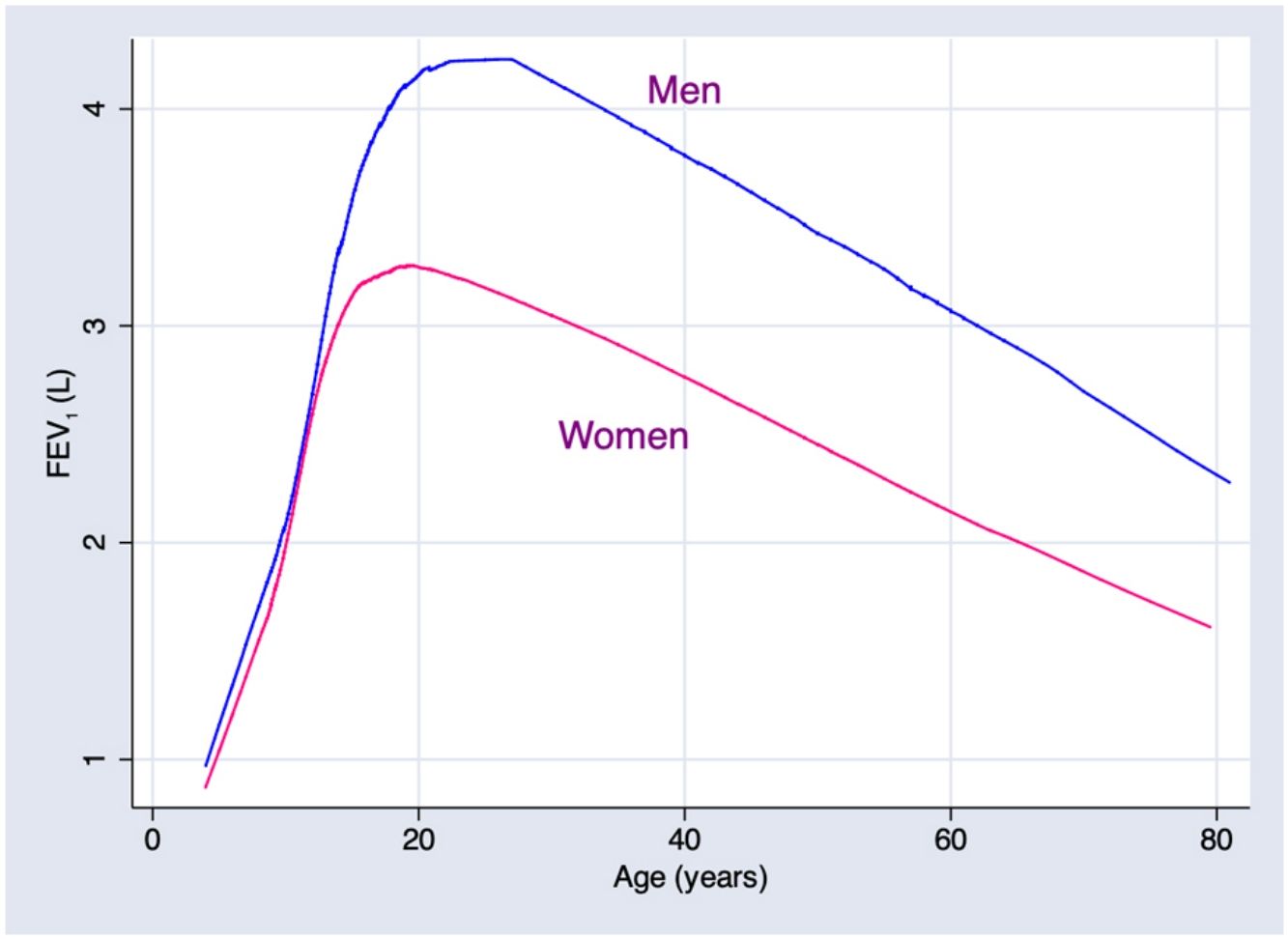
Predicted values of reference equations for FEV1.
Lines represent predicted values with spirometric reference equations: LMS equation (continuous line), Pérez Padilla (broken line), GLI equation (long dash, short dash) and linear regression model (very short dash). LMS model: generalized additive model for location, scale and shape, LMS method; LR: linear regression model; FEV1: forced expiratory volume in 1s; FVC: forced vital capacity; FEV1/FVC: ratio of FEV1 to FVC.
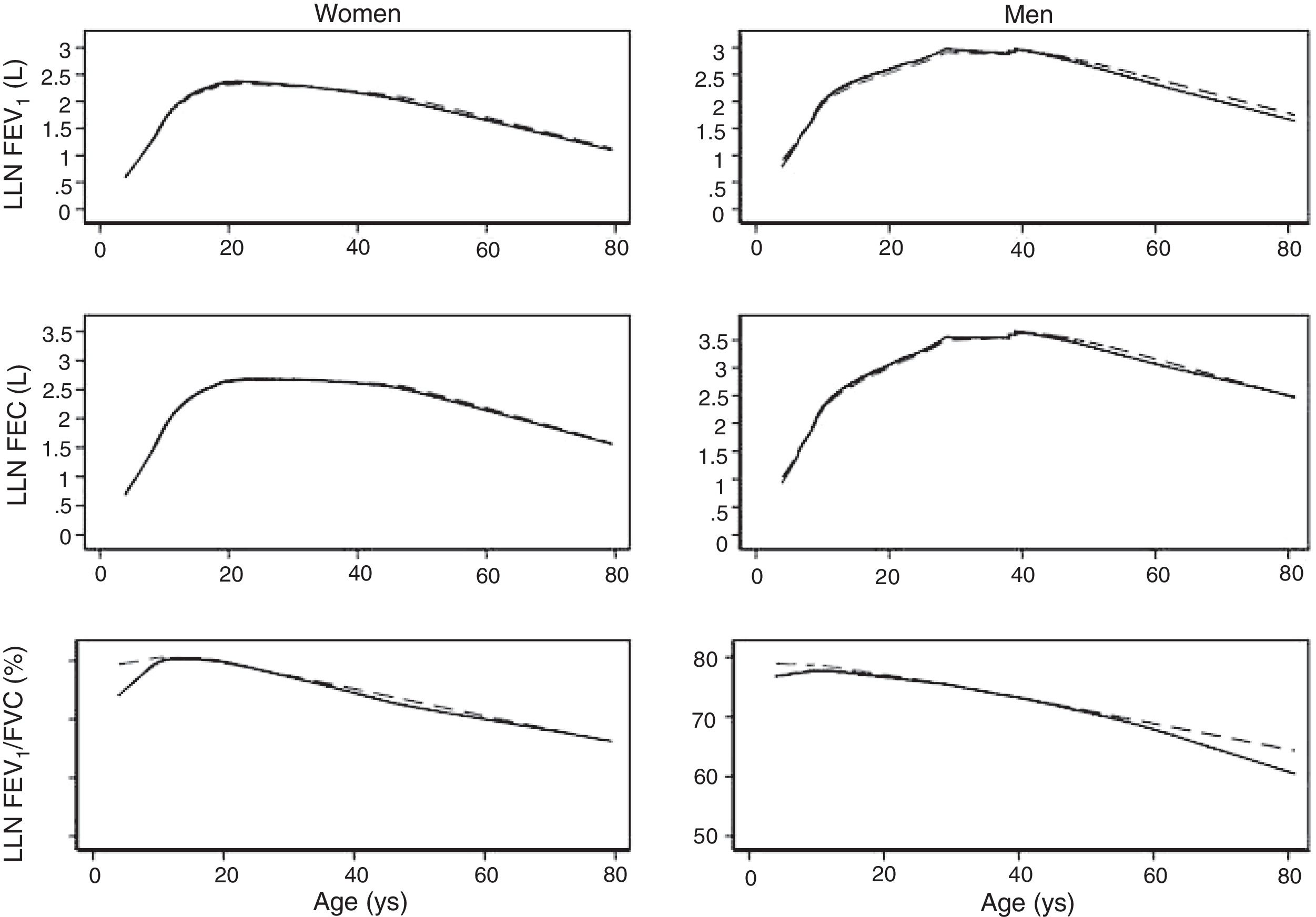
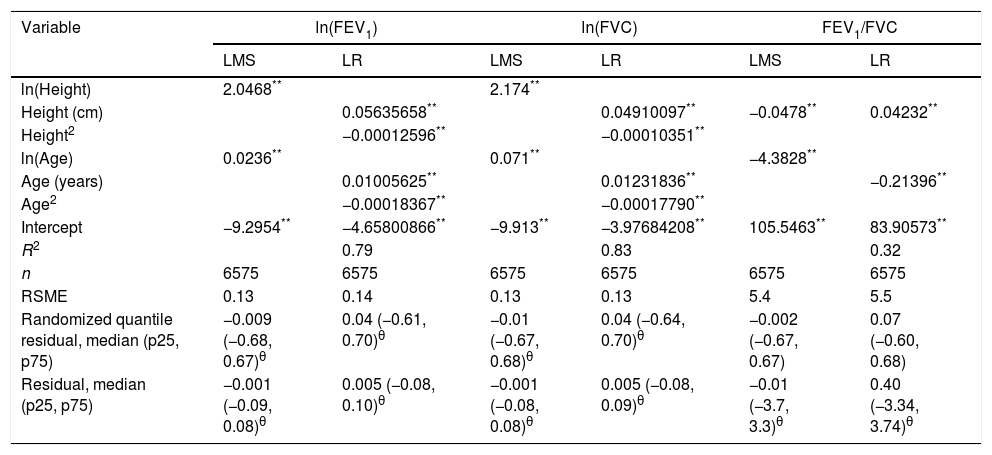
We fitted the LMS and linear regression models and then estimated the quantile (standardized) residuals for each one, eliminating observations if the Z-score was <−3 or >+3. After that procedure, the models were fit again. A total of 89 observations for women and 205 for men were discarded as outliers. Tables 3 and 4 display the LMS models of lung function (FEV1, FVC and their ratio) based on height and age for women and men, respectively. We also obtained a smooth fit over the whole age range using penalized B-splines, that allow the dependent variable to vary smoothly throughout the age, especially the lung function ascent and descent. This variables are contained in an excel file (lookuptableMx.xls). In the supplemental material is described how to use the reference equations and splines to compute predicted values, lower limit of normal (LLN) and Z-scores. Tables 5 and 6 compare the LMS and linear models and root mean squared error, which was quite similar in both sets of models for both women and men. Table A.1 shows the spirometric values of participants expressed as the Z-scores from two reference equations from Mexico and the international GLI equation.4,10,11
LMS models for spirometric variables in the female subjects.
| Variable | M | S | L | M | S | L | M | S | L |
|---|---|---|---|---|---|---|---|---|---|
| ln(FEV1) | ln(FEV1) | FEV1 (L) | ln(FVC) | ln(FVC) | FVC (L) | ln(FEV1/FVC) | ln(FEV1/FVC) | FEV1/FVC | |
| ln(Height) | 2.0351** | 2.0625** | |||||||
| Height (cm) | −0.00008 | ||||||||
| ln(Age) | −0.0115** | 0.085** | −0.02 | 0.0442** | 0.051** | −0.25 | −0.05940** | 0.0024 | 0.19 |
| Intercept | −9.2300** | −2.402** | 1.23* | −9.3880** | −2.272** | 1.61** | 4.65362** | −2.8602** | 2.84** |
| n | 2965 | 2965 | 2965 |
FEV1: forced expiratory volume in 1s, expressed in liters; FVC: forced vital capacity in liters; FEV1/FVC: ratio of FEV1 to FVC as a fraction. LMS model: generalized additive model for location, scale and shape, LMS method.
LMS models for spirometric variables of the male subjects.
| Variable | M | S | L | M | S | L | M | S | L |
|---|---|---|---|---|---|---|---|---|---|
| ln(FEV1) | ln(FEV1) | FEV1 (L) | ln(FVC) | ln(FVC) | FVC (L) | FEV1/FVC | FEV1/FVC | FEV1/FVC | |
| ln(Height) | 2.0468** | 2.174** | |||||||
| Height (cm) | −0.0478** | ||||||||
| ln(Age) | 0.0236** | 0.108** | 0.37** | 0.071** | 0.094** | 0.34** | −4.3828** | 0.00119 | 0.34 |
| Intercept | −9.2954** | −2.430** | −0.22 | −9.913** | −2.424** | −0.36 | 105.5463** | 0.05870** | 2.25** |
| n | 6575 | 6575 | 6575 |
LMS model: generalized additive model for location, scale and shape, LMS method. Age expressed in years. FEV1: forced expiratory volume in 1s, expressed in liters; FVC: forced vital capacity in liters; FEV1/FVC: ratio of FEV1 to FVC as a fraction; RMSE: root-mean-square error.
*p<0.05.
Adjustment of LMS and linear regression models for spirometric variables for the female subjects.
| Variable | ln(FEV1) | ln(FVC) | ln(FEV1/FVC) | |||
|---|---|---|---|---|---|---|
| LMS | LR | LMS | LR | LMS | LR | |
| ln(Height) | 2.0351** | 2.0625** | ||||
| Height (cm) | 0.0575872** | 0.0505208** | −0.00008 | 0.0010022** | ||
| Height2 | −0.0001315** | −0.0001110** | ||||
| ln(Age) | −0.0115** | 0.0442** | −0.05940** | |||
| Age (years) | 0.0098811** | 0.0140743** | −0.0029468** | |||
| Age2 | −0.0002149** | −0.0002325** | ||||
| Intercept | −9.2300** | −4.7751014** | −9.3880** | −4.1232304** | 4.65362** | 4.3845851** |
| R2 | 0.82 | 0.82 | 0.36 | |||
| n | 2965 | 2965 | 2965 | 2965 | 2965 | 2965 |
| RSME | 0.12 | 0.13 | 0.12 | 0.13 | 0.06 | 0.06 |
| Randomized quantile residual, median (p25, p75) | −0.013 (−0.66, 0.66) | 0.032 (−0.61, 0.69) | −0.004 (−0.67, 0.67) | 0.039 (−0.64, 0.68) | −0.01 (−0.67, 0.69) | 0.08 (−0.57, 0.7)θ |
| Residual, median (p25, p75) | −0.001 (−0.08, 0.08)θ | 0.004 (−0.08, 0.09)θ | −0.0004 (−0.08, 0.07)θ | 0.004 (−0.081, 0.086)θ | −0.06 (−3.52, 3.27)θ | 0.43 (−3.09, 3.866)θ |
LMS model: generalized additive model for location, scale and shape, LMS method. LR: linear regression model; FEV1: forced expiratory volume in 1s, expressed in liters; FVC: forced vital capacity in liters; FEV1/FVC: ratio of FEV1 to FVC as a fraction; RMSE: root-mean-square error.
*p<0.05.
LMS and LR models for spirometric variables for the male subjects.
| Variable | ln(FEV1) | ln(FVC) | FEV1/FVC | |||
|---|---|---|---|---|---|---|
| LMS | LR | LMS | LR | LMS | LR | |
| ln(Height) | 2.0468** | 2.174** | ||||
| Height (cm) | 0.05635658** | 0.04910097** | −0.0478** | 0.04232** | ||
| Height2 | −0.00012596** | −0.00010351** | ||||
| ln(Age) | 0.0236** | 0.071** | −4.3828** | |||
| Age (years) | 0.01005625** | 0.01231836** | −0.21396** | |||
| Age2 | −0.00018367** | −0.00017790** | ||||
| Intercept | −9.2954** | −4.65800866** | −9.913** | −3.97684208** | 105.5463** | 83.90573** |
| R2 | 0.79 | 0.83 | 0.32 | |||
| n | 6575 | 6575 | 6575 | 6575 | 6575 | 6575 |
| RSME | 0.13 | 0.14 | 0.13 | 0.13 | 5.4 | 5.5 |
| Randomized quantile residual, median (p25, p75) | −0.009 (−0.68, 0.67)θ | 0.04 (−0.61, 0.70)θ | −0.01 (−0.67, 0.68)θ | 0.04 (−0.64, 0.70)θ | −0.002 (−0.67, 0.67) | 0.07 (−0.60, 0.68) |
| Residual, median (p25, p75) | −0.001 (−0.09, 0.08)θ | 0.005 (−0.08, 0.10)θ | −0.001 (−0.08, 0.08)θ | 0.005 (−0.08, 0.09)θ | −0.01 (−3.7, 3.3)θ | 0.40 (−3.34, 3.74)θ |
LMS model: generalized additive model for location, scale and shape, LMS method. LR: linear regression model; FEV1: forced expiratory volume in 1s, expressed in liters; FVC: forced vital capacity in liters; FEV1/FVC: ratio of FEV1 to FVC as a fraction; RMSE: root-mean-square error.
*p<0.05.
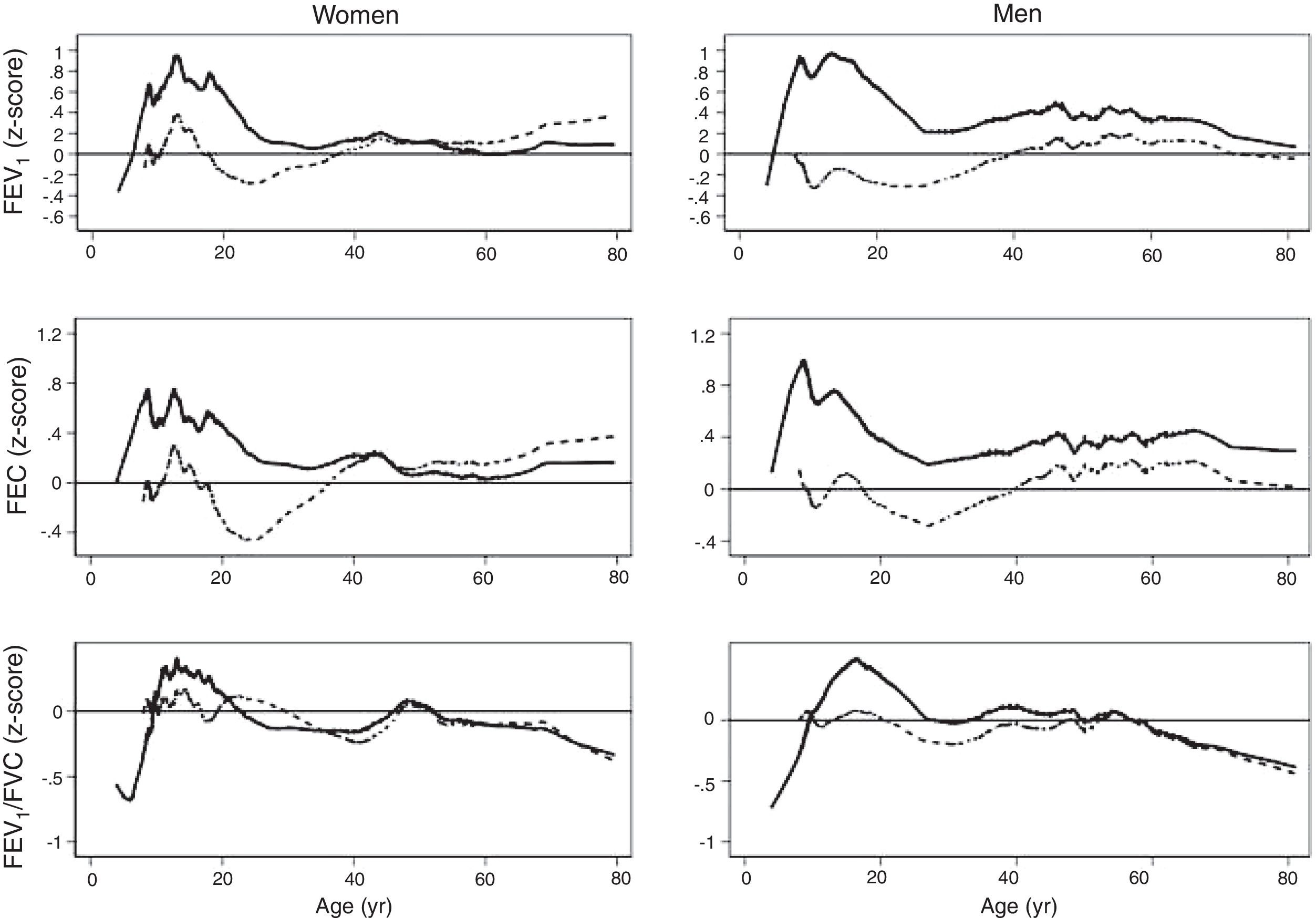
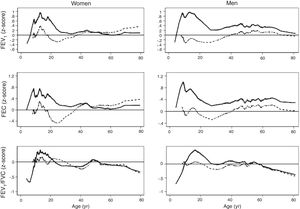
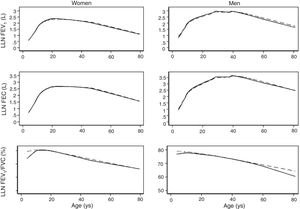
The spirometric values of participants expressed as Z-scores of the GLI reference values were higher than those expressed as Z-scores of the Perez-Padilla study by 0.3–0.5 SD for FEV1 and FVC for both women and men. The differences in FEV1/FVC among the equations were minor. Fig. 2 shows that the spirometric measurements expressed as GLI Z-scores were higher than those for the other equations for both genders and for children and adults, but especially in children. The equations from the Perez-Padilla et al. study were closer to the zero Z-score in children and adults. The lower limit of normal and the individuals below the 5th percentile estimated by the LMS and by regular multiple regression were also very similar (see Table A.2 and Fig. 3). A Wilcoxon matched-pairs signed-rank test was carried out in order to compare the medians of residuals and randomized quantile residuals between LMS and linear regression models. We found statically differences in FEV1, FVC and FEV1/FVC in both female and males of the residual's models (p<0.05). The residuals of the LMS and linear regression models were also compared for each spirometric variable by age group (Figure A.1–A.6, Tables A.3 and A.4).
We describe a continuous analysis of spirometric lung function growth and aging, by compilation of spirometric reference studies comparing the LMS methodology with standard linear regression, and found that although LMS methodology offer advantages over standard multiple linear regression, these were minimal, as long as models to predict log(FEV1), log(FVC) and FEV1/FVC include quadratic terms. The differences in the 5th percentile between the two methods were also minimal, as seen in Table A.2 and Fig. 3.
In addition, results obtained from Mexican populations residing at an altitude of 2240m, were, for any given height, generally above the levels found in North American and European populations, reported by international GLI equations. This is a consequence of a different relation between height and chest volume, in general well-preserved chests in people with diminished height. This response has been described, in fact, for populations that suffer environmental stress due, for example, to malnutrition,16,17 though the contribution of residing at high altitudes18–22 or other unknown factors cannot be ruled out.
These results for mean lung function, dispersion and lower limits of normal, usually the 5th percentile, are thus more reliable and comprehensive than when study groups are separated at about 18 years of age. Several previous studies have demonstrated the interpretative advantages of methods based on percentiles and standard deviations from the average,7,23,24 compared to using percentages of predicted values.1 The apparent complexity of incorporating these data into spirometers presents no obstacles to the microprocessors included in modern spirometers. Reported results require validation in different Mexican populations to identify ethnic or socioeconomic groups that may have better or worse adjustments.
This study is based on a compilation of tests performed at different times and using 3 distinct types of spirometers, though all devices were high-quality instruments that satisfy international standards and calibration was verified daily. Also, participants were obtained through different approaches, including population-based sources (the PLATINO study), a random sample of schools (the EMPECE study), and convenience samples in the remaining. On the other hand, the criteria applied to determine that participants were healthy were similar in all studies: non-obese never-smokers who were free of respiratory symptoms and had no previous diagnoses of respiratory diseases. In addition, spirometry tests were performed by expert technicians following international quality standards. All age groups had a considerable number of participants, but decreased above 60 years of age, reducing the precision of estimates for older individuals.
Compilation of studied groups at different times, offers difficulties as characteristics often change with time (cohort effect), but for this and other reasons, average lung function and population dispersion, may change with time and results have to be considered temporary and will have to be updated progressively. On the other hand, one of the objectives of our work, not affected by time or cohort effect, was to compare possible advantages of the LMS method to linear regression, to obtain a continuous equation, and we observed that the LMS method is more complex and, reduces only a very small proportion of the adjustment error, and in addition, it is clear that GLI equation does not fit properly the studied population. It is important to acknowledge the need of validation in other populations and in different ethnic groups the proposed LMS and linear regression equations.
ConclusionThe continuous reference equations for a Mexican population estimated by the LMS technique provide slight advantages over the continuous equations calculated by more traditional equations obtained with log-transformed spirometric variables and crude and squared predictors. Due to the characteristics of current spirometry devices and microprocessors, implementing continuous LMS-type equations presents no difficulty. For a given height, spirometric values in the studied population were higher than those described in the international GLI equations.
Conflict of interestThe authors declare no conflict of interest.